Compressive Acceleration of Solar Energetic Particles (SEPs) Within Coronal Mass Ejections (CMEs)
PDF version

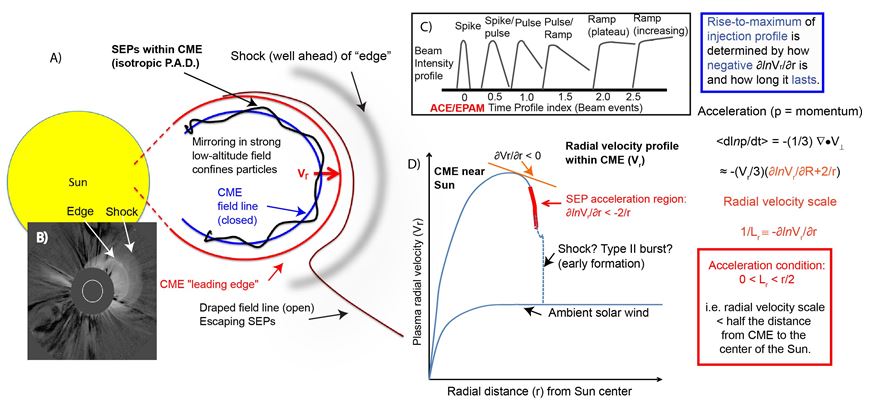
Analysis of the Solar Cycle 23 ACE/EPAM database revealed a continuous morphology (summarized in Panel C) of the injection history of ~200 magnetically well-connected SEP >40 keV electron events and associated CMEs [Haggerty and Roelof, AIP Conf. Proc., 1183, 3, 2009]. The explanation for this simple pattern may lie in a completely general expression [Roelof, IOP J. Phys. Conf. Series 642, (2015) 012023] for the fractional time-rate-of-change of any individual charged particle's momentum (dlnp/dt), independent of any properties of the particle.

When the SEP velocity distribution is isotropic, the acceleration rate <dlnp/dt> = -(1/3)∇•V_⊥, averaged over pitch-cosine, involves only the compression (divergence) of the component of the plasma velocity transverse to the magnetic field (∇•V_⊥). The isotropy condition is satisfied for SEPs on the closed magnetic field lines within the body of a CME, as sketched in Panel (A). There can be strong compression of the plasma behind the leading "edge" of the CME, well separated from the driven shock, as revealed in Panel B, a SOHO/LASCO white-light coronagraph image of a CME associated with an "SEP-rich" event [Kahler and Vourlidas, JGR 110, A12S01, 2005]. As outlined in the equations at the right of the Figure, SEPs will be accelerated if there is a sufficiently negative radial gradient (δV_r/δr < -2V_r/r) in the radial plasma velocity. As illustrated by the generic sketch of V_r vs. r in Panel D, there will be a region within the nose of the CME where δV_r/δr <0, because the pressure-driven velocity radial profile must always steepen Sunward of the CME leading edge. As to whether it steepens sufficiently for acceleration (∇•V_⊥<0), the equations reveal that the critical acceleration parameter is the radial scale (1/L_r=-δlnV_r/δr) of that radial velocity gradient.

Based on images such as Panel B, we expect small values of L_r ~0.1 RS (expressed in solar radii) at the "edge". For a CME at r=2RS, the formulas predict an e-folding time for momentum increase of 3.9 minutes, for any particle species at any energy (while it is in the compression region of the CME). Then the duration of the rise-to-maximum of the SEP injection profile (Panel C) will be ordered by how long the strong compression region lasts (where δV_r/δr < -2V_r/r). Brief compressions will produce brief "Spikes", longer ones will produce longer "Pulses", but when a strong shock forms ahead of the CME "edge", compression-accelerated particles will synergistically interact with the shock, thus extending the acceleration process well out into the solar wind, producing "Ramps", the most intense and longest-lasting SEP injections observed.

This item was contributed by E. C. Roelof, D. K. Haggerty, and A. Vourlidas, Johns Hopkins University/Applied Physics Laboratory. Address questions and comments to

ACE News Archives

Subscribe to ACE News

ACE Homepage

Last modified 22 Oct 2015.